Kolam

By Lavannya Suressh, 8/26/2023.

Chapter 1: Introduction
Concept and Significance

Arts and culture have existed as essential daily practices in South Asia for a very long time. In this paper, we will look at Kolams, a South Asian art form which has its precedents in mathematical learning; I will collapse the dichotomy between ‘traditional’ and ‘modern’ by approaching this art form with programming and code. The complex relationship between the physical and the digital domain has been expressed through tools, techniques and technologies associated with their development. This relationship is less complementary than it is co-dependent: new capabilities in digital fabrication enable the realization of sophisticated tools of design computation, while new affordances in design computation inspire innovation in digital fabrication. The level and quality of co-dependency, whereby design computation enables control and manipulation over the digital domain, as digital fabrication affords control and manipulation over the domain of the physical; signifying determines their l synergy Moreover, the ability to reduce, and even eliminate, the mismatch between digital and physical design tools will ultimately result in fully integrated platforms for design and designers with few ‘acts of translation’ between the physical and the digital. But for designers leading the transition from the digital age to the biological age-the challenge to author a cross-domain auxiliary language continues, as do its associated acts of translation. As we face the challenge to shift between and across fields–their associated units and modes of expression-we must find ways by which to mediate between the physical, the digital and the biological, enabling new ecological perspectives.

It is interesting how an artwork done from memory on a daily basis can have such a logical structure with deep conceptual learnings associated with it. Pulli kolam is a ubiquitous art form in south India. It involves drawing a line looped around a collection of dots (pullis) placed on a plane such that three mandatory rules are followed: all line orbits should be closed, all dots are encircled, and no two lines can overlap over a finite length. The mathematical foundation for this art form has attracted attention over the years. With every sunrise, women wash the floor in front of the houses, and using rice flour, place the dots and draw a kolam largely from memory. The kolams become increasingly complex, with a larger number of dots and more intricate line orbits. Remembering the dot configurations and line orbits is a daily exercise in geometric thinking. The process is immensely pleasurable, especially when a kolam is successfully completed with no loose ends. Throughout history there were gendered exclusions in tech centric fields and the intelligence required to draw increasingly complex kolams have been undervalued. Exploring the form through technology, mathematical structures and taking it as a cultural precedent to learn mathematical concepts from can play an important role valuing contributions to art science and technology from non-western cultures, and from women.

With our mathematical learnings, it is important to take examples and precedents from our cultures as practices. Pulli Kolam, a south indian art form is a great way to study fractals, geometry, and looping patterns. Approaching this through code helps enshrine the intricacy of practices, which have, for a very long time due to colonialist epistemologies, seen as ‘primitive’ or ‘primordial’.

Looking at Kolams a traditional South Indian art form beyond something that’s a daily ritual. Taking it as a valued precedent for mathematical learning concepts exploring rules that limit while encouraging creativity at the same time. Approaching this art form with code to create generative code-driven art forms following the same traditional rules and structures show that there is more intelligence required to perform this than credited for and a way of looking at kolams alongside mainstream generative art. Exploring the form through technology, mathematical structures can play an important role valuing contributions to art science and technology from non-western cultures and women.

Chapter 2: Context
Culture and process

Taking a clump of rice flour in a bowl (or a coconut shell), the kōlam artist steps onto her freshly washed canvas: the ground at the entrance of her house, or any patch of floor marking an entry point. Working swiftly, she takes pinches of rice flour and draws geometric patterns: curved lines, labyrinthine loops around red or white dots, hexagonal fractals, or floral patterns resembling the lotus, a symbol of the goddess of prosperity, Lakshmi, for whom the kōlam is drawn as a prayer in illustration. The making of the kōlam itself is a performance of supplication. The artist folds her body in half, bending at the waist, stooping to the ground as she fills out her patterns. Many kōlam artists see the kōlam as an offering to the earth goddess, Bhūdevi, as well.
Kolam means “beauty”. The simplest form of the kolam is the pulli kolam or “dotted kolam”.6 Dots of rice flour are placed in a grid-like framework, which are then joined to take the form of a symmetrical shape or a regular polygon. Symmetry was of key importance to the kolam artist. It can be compared to fractals in mathematics that can get increasingly complex across scales. These small patterns can be scaled up and interconnected in many ways and the possibilities maximize. This can be approached with code in 2 ways as we’ll see through the rest of this paper.

The kolam tradition of Tamil Nadu has persisted for hundreds of years and remains a common practice among women in cities as well as in rural areas, among those who are university educated as well as those less schooled. In recent years, instead of rice, women have often substituted commercially available stone powder, chalk, or ink for creating the designs.

Exploring the techniques of skilled kolam artists offers insights into the intricate thought processes behind kolams, loop figures, and the cognitive aspects of comprehending mathematical concepts. I collaborated with Mrs. Muthulakshmi Sankaran from Chennai, a dedicated kolam artist who sees it as a mental exercise. Through our collaboration, she guided me in deconstructing her creative process and the purpose behind each design. I then leveraged these insights to develop a computer algorithm, translating her methods into a detailed, step-by-step programmatic instruction set.

She used different colors to delineate each closed loop drawing within the grid, thus creating a clear visual distinction between each step and process. This use of colors served a functional purpose in understanding the progression and intricacies of her artistry.

By assigning unique colors to specific sections or elements of the kolam, Mrs. Muthulakshmi Sankaran effectively conveyed the sequential nature of her creative process. This technique allowed for a more comprehensive understanding of how each element contributed to the overall design, making it easier to discern the layering and development of the kolam as it evolved step by step.

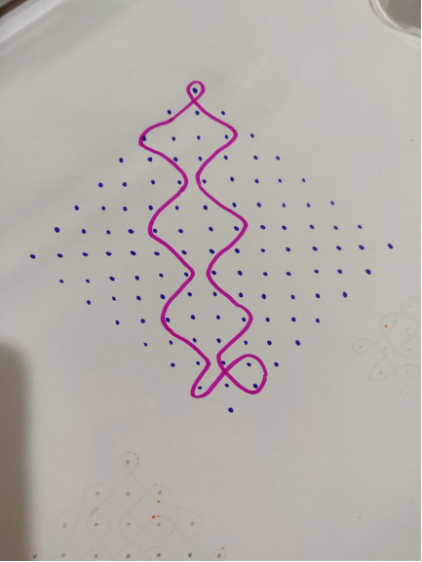
Her process begins by creating a solitary closed-loop pattern that gracefully traverses the grid diagonally. Subsequently, this singular design is duplicated in a symmetrical fashion across the grid, resulting in a 4-fold symmetry. This approach unveils two noteworthy observations that I discerned during my exploration.

Firstly, it highlights the rich variety of movements achievable when traversing diagonally across the grid. This dynamic aspect of her technique showcases the versatility and creativity inherent in the art of kolam-making.

Secondly, this process also underscores a fascinating limitation: when incorporating curves around a central dot, there are only three distinct approaches one can take. This intriguing constraint speaks to the nuanced yet structured nature of kolam design, where seemingly boundless creativity thrives within a defined framework.

Chapter 3: Methodology
A Journey into Code

There are a set of rules that follow what is specifically identified as a kolam. They are as follows:

(1) Loop drawing-lines, and never trace a line through the same route.
(2) The drawing is completed when all points are enclosed by a drawing-line.
(3) Straight lines are drawn along the dual grid inclined at an angle of 45°.
(4) Arcs are drawn surrounding the points.
(5) Smooth drawing-lines. Lines should not bend in a right angle.

The rules and conventions will be explained in further detail going forward.

Method 1: Looping Kolams across a grid

In this method, we will replicate the core method of how the Kolam art is done. The Dots are placed in a grid-like structure linearly across a diagonal first as a framework and go around in loops with arcs and straight lines following patterns and symmetry. The grid is however big or small you want the kolam to be.
For the purpose of keeping simple, we’ll go with a 4-fold symmetry i.e., we start with keeping a square (everything is rotated by 45 degrees) in the middle and the pattern repeats on all 4 sides.

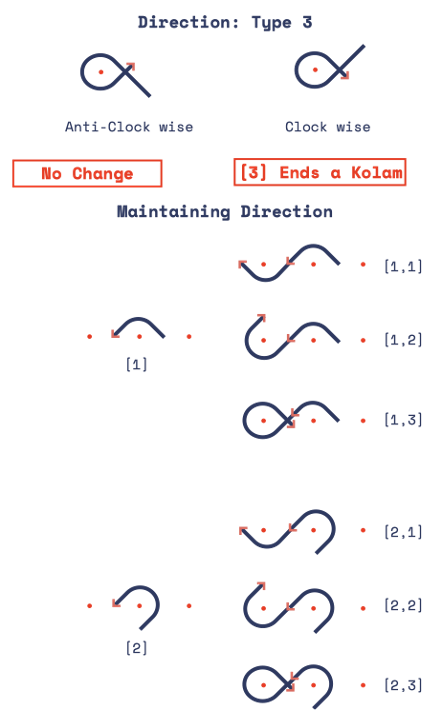
There are 3 types of arcs that make up the single line drawing of a Kolam. They are all based on having 1, 2, and 3 curved sides of a square. The radius of the curved sides is half the side-length of the square. Assigning these numerical values to each type can be processed by the looping function. 

There are a set of rules that we follow while traversing across the grid to make up what distinctively identifies as a Kolam. The rules are illustrated in fig(i) and fig(ii) below showing two case scenarios:

1. If the direction of traversing through the grid is the same.
2. If you’re traversing to the next row of dots.

A kolam always ends with loop type 3 maintaining the rule of leaving no loose ends behind.

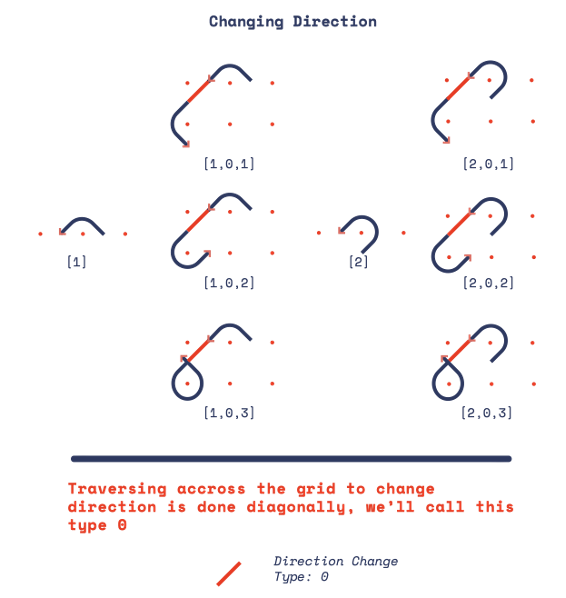
Type 0 is a straight line that needs to be drawn to start looping Kolams in the next grid.
The forward looping is straightforward with numerical values 0,1,2 and 3. This can be inputted into the system in the form of an array.

Since a Kolam ends at loop type “3” so the input arrays are limited to types 0,1 and 2 and appended at the end with type 3.

Looping Back with a Grid:

We follow a set of rules to loop back after we get to loop type “3” to form the closed loop structure of a Kolam. It is illustrated in fig(iv) below.

1. Loop type 1 is looped back with loop type 1.
2. Loop type 2 is followed back with loop type 0.
3. Loop type 0 is followed back with loop type 1.

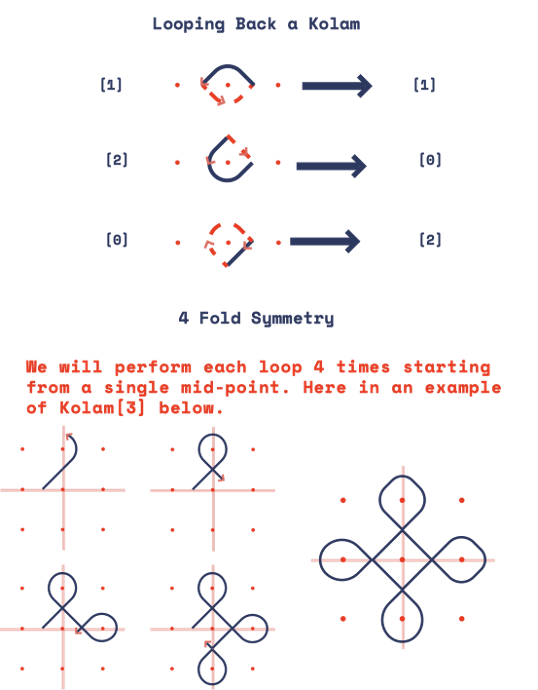
Kolam [3] is the most basic type of Kolam, the kolams get increasingly complex based on the length of the array entered. Following these simple rules, we will develop a recursive function to make a Kolam.

Below are the few examples of Kolams we can derive with the method discussed above.

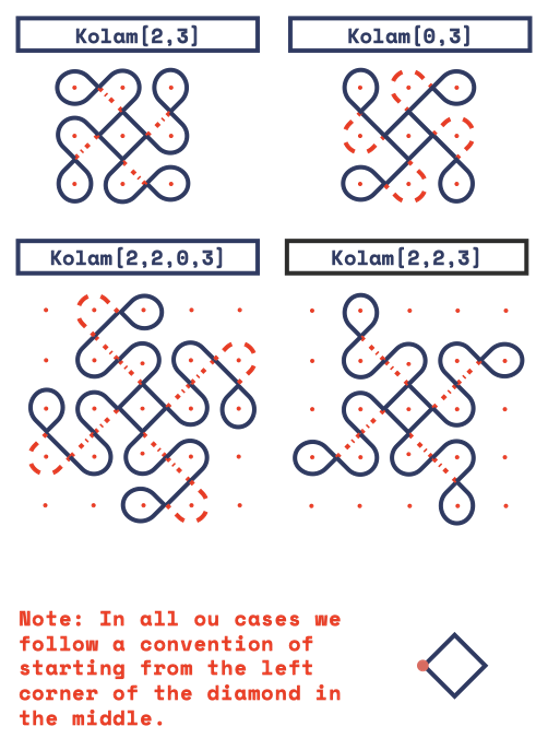
A Recursive function where you go around the grid in a user input directing how you go around the grid with rectangles with a radius of curvature in different combinations of the sides and the code computes how this is looped back to form a kolam. This method has a lot more scope in terms of scalability and application of data, artificial intelligence etc. while taking kolams forward.

Each number corresponds to one block of code that does the following as shown in fig(v):

There are some import mathematical concepts we can explore through Kolams:

1. Symmetry
2. Fractals
3. Array grammars
4. Infinity

Method 2: Kolam Tiles and Shapes

Another way we can look at kolams is based on the shapes that constitute it. This is a method derived from looking at the outlook of what a finished kolam looks like and how it can be represented.

We will visually approach it by placing tiles in a framework. There are 6 types of tiles in different orientations shown in fig(vi)

These shapes are based on curved sides of the square in different permutations. Let’s denote curved sides as 1 and pointed sides as 0. Taking a clockwise convention, the corners a, b, c, and d can take binary values of 0 and 1.

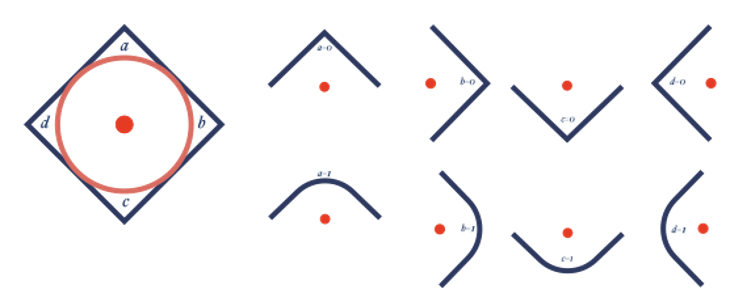
The framework of the grid is similar to a cartesian system, but we consider only the coordinates from a diagonal. The framework is illustrated below in fig(vii).

Each side can have two possible values and there are 4 sides so totally there are 2x2x2x2 permutations of shapes. This can be compared to Hexadecimals with 4 bytes of data each taking either a value of 0 or 1.
Figure(viii) Shows all the permutations of shapes. There are 16 shapes that make up a kolam and can be denoted with Hex codes.

The grid where we place our kolam shapes is important to understand and represent the kolam structure. It is similar to a simple cartesian coordinate system in a diagonal space. We can structure a Kolam through this with a few simple rules. fig(ix) Shows that grid structure and the corresponding coordinate values. Imagine a regular cartesian system rotated clockwise by 45 degrees. This is the convention we are following here.

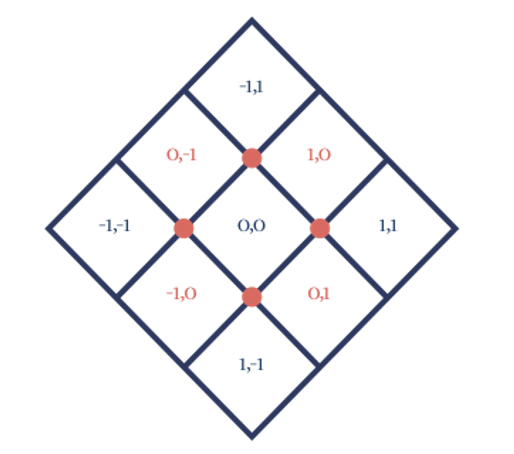
We have the constant (0,0) space where usually the symmetry of the kolam is around, We will look at how the Kolam rules conform around the grid at any given value x and y. Fig(x) shows the grid structure.

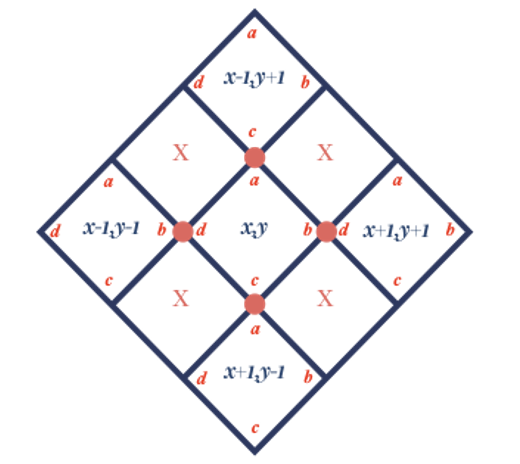
The rules that we follow while constructing a Kolam are the following:

1. The sum of the x and y value should be divisible by 2.
2. Adjacent blocks have the same value at the point the joining point to maintain the single line drawing rule.
3. Endpoints of Kolams must end with a “1.”

axy refers to the “a” value of the (x,y) coordinate of the tile, The rules are for all the valid tiles around it. They are Illustrated in fig(xi) below:

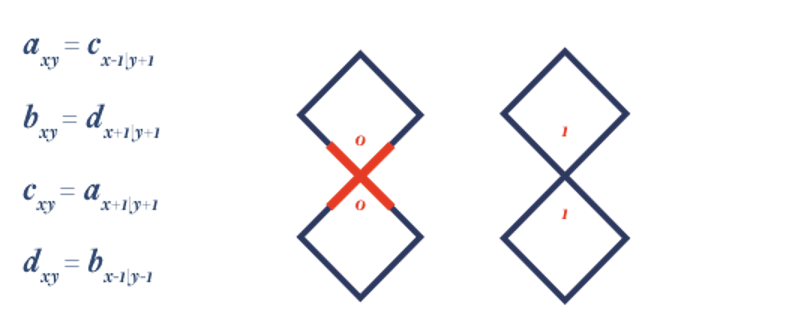
This is very similar to data communication in 4-bit computers where the bit values need to match to progress through making a Kolam. Fig(xii) shows a few examples of generated Kolams. Although this can be extended in any way following the given set of rules, maintaining some level of symmetry is part of the aesthetic of what makes up a Kolam. This generative method of computing Kolams across a space can have a lot of scope for understanding data and communication.

In computer architecture, 4-bit integers, or other data units are those that are 4 bits wide. Also, 4-bit CPU and ALU architectures are those that are based on registers, or data buses of that size. Memory addresses for 4-bit CPUs are generally much larger than 4-bit, such as 12-bit or more, while they could in theory be 8-bit. A group of four bits is also called a nibble and has 2⁴ = 16 possible values.
Some of the first microprocessors had a 4-bit word length and were developed around 1970. Traditional 4-bit computers are by now obsolete, while recent quantum computers are 4-bit, but also based on qubits, such as the IBM Q Experience. See also: Bit slicing#Bit-sliced quantum computers.

Chapter 4: Evaluation

We can see how we’ve used technology to approach and understand a traditional artform. In context it can first be used to value the contributions to mathematics and computing from marginalized groups. This attempt to understand Kolams and implement it with 2 different programming languages. One of the important key learnings we can take is to take a deep look into culture and traditional forms and their contributions.

The mathematical and scientific explanations would not only attract the young generation to practice the art but would also generate curiosity amongst scholars to preserve the tradition.

It is, however, difficult to distinguish the complexity of Kolam at glance. Creating a Kolam pattern is expected to be useful for activating/training the human brain. It is a wonder that a woman with no math knowledge (except counting) is able to draw any type of complex pattern without much effort. They show their perfection in geometrical presentation, symmetry, straight lines, curves etc., girls capture, encode, and decode the image in their memory with much clarity before reproducing it on the ground. Kolam can be called an “ethno-mathematical” activity.

As computer scientists have tried to capture kolam figures with picture languages, they have highlighted the richness of the kolam structures and their algorithmic nature? In other words, the orderly, step-by-step way they are built. The languages do not necessarily replicate how the women of Tamil Nadu conceive of and draw the kolam figures. Nevertheless, they underscore the fact that the kolam, and particularly the families of kolam, are more than just a collection of individual pictures; systematic procedures and techniques unify them. The kolam tradition has also provided an unusual opportunity for the computer scientists. There may be no better way to examine an academic construct than to apply it to examples from a tradition and culture outside the one in which the construct arose. But in addition, the computer scientists sought to learn from the figure makers and integrated what they learned into the theory and practice of their own field. This recent phase in the history of the kolam tradition showcases how mathematical ideas can move beyond their traditional boundaries, interact with an academic endeavor, and in fact contribute to it.